viernes, 29 de marzo de 2019
jueves, 28 de marzo de 2019
Pi (final): la cuadratura del círculo
Los matemáticos de la antigua Grecia se inventaron el “juego de la regla y el compás” en el que, siguiendo unas determinadas normas, había que construir figuras geométricas, dividir segmentos o ángulos en varias partes iguales, etc, utilizando una regla y un compás. No vamos a entrar en detalles pero una de las normas es que la regla no tiene marcas, no sirve para medir, sólo se puede utilizar para pintar segmentos o rectas uniendo dos puntos.
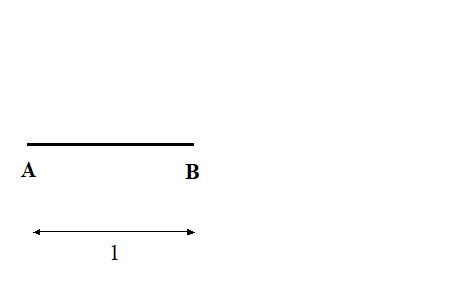
Una de las modalidades del “juego de la regla y el compás” era la de construir números. La idea es sencilla: partimos de un papel en el que tenemos dibujado un segmento de longitud 1 (da igual la unidad; por comodidad ponemos nombre a los extremos, A y B):
y, utilizando un compás y una regla (insisto, sin números, no podemos medir con ella), tenemos que intentar construir segmentos de la longitud que nos digan. Vamos a ver tres ejemplos:
1) Construir un segmento de longitud 2. El 2 sale muy fácil: prolongamos por la derecha el segmento original con la regla, pinchamos con el compás en el punto B, lo abrimos hasta el punto A y lo giramos y marcamos el punto C. Desde A hasta C el segmento resultante mide 2.
2) Construir un segmento de longitud 0'5. ¡Seguro que lo habéis hecho alguna vez! Simplemente se trata de dibujar la mediatriz del segmento que nos dan:
Una de las modalidades del “juego de la regla y el compás” era la de construir números. La idea es sencilla: partimos de un papel en el que tenemos dibujado un segmento de longitud 1 (da igual la unidad; por comodidad ponemos nombre a los extremos, A y B):
1) Construir un segmento de longitud 2. El 2 sale muy fácil: prolongamos por la derecha el segmento original con la regla, pinchamos con el compás en el punto B, lo abrimos hasta el punto A y lo giramos y marcamos el punto C. Desde A hasta C el segmento resultante mide 2.
 |
| Siguiendo la misma idea sería inmediato construir segmentos de longitudes 3, 4, 5, 6... |
2) Construir un segmento de longitud 0'5. ¡Seguro que lo habéis hecho alguna vez! Simplemente se trata de dibujar la mediatriz del segmento que nos dan:
3) Construir un segmento de longitud raíz de 2. Lo tenemos a tiro aprovechando los ejemplos anteriores:
y ya lo tenemos, si recordamos el Teorema de Pitágoras:
Volvamos al dibujo anterior:
Los griegos jugaron bastante a este juego y lograron construir un montón de números... hasta que lo intentaron con nuestro querido p.
La cuestión es: partiendo de un segmento de longitud 1, ¿podemos construir con regla y compás un segmento que tenga longitud p?
En realidad este problema se puede plantear de otra manera más glamurosa que es la que le da nombre: dado un círculo de radio 1, ¿podemos construir con regla y compás un cuadrado que tenga su misma área?
En 1882, más de 2000 años después de que hubiera sido planteado, tras haber resistido a los mejores matemáticos del mundo durante dos milenios, el problema fue derrotado: Carl Louis Ferdinand von Lindemann (Lindemann para los amigos) se ganó la inmortalidad demostrando que NO, que LA CUADRATURA DEL CÍRCULO ES IMPOSIBLE (y por eso, igual ya lo habéis oído alguna vez, es por lo que se emplea el dicho, "eso es la cuadratura del círculo", para referirse a algo que es imposible de hacer).
Por cierto, id sacando los pañuelos de papel, porque no me cabe ninguna duda de que con lo que ahora mismo os voy a decir vuestros ojos se van a inundar de lágrimas de emoción sincera: ¿sabéis cómo consiguió resolver Lindemann el problema de la cuadratura del círculo? Con ecuaciones. Y ahora viene lo mejor, ¿sabéis qué tipo de ecuaciones? ¡Ecuaciones con polinomios!
Y cuando se os pase la emoción, Nuria, Paula, Fernando, Miguel, Álex y Adrián, aquí va el último reto (mandadme una imagen por Instagram o enseñádmelo en clase):
Reto IV de p. Construye con regla y compás:
y ya lo tenemos, si recordamos el Teorema de Pitágoras:
Volvamos al dibujo anterior:
 |
| ¿Cuánto mide el segmento DC? |
Los griegos jugaron bastante a este juego y lograron construir un montón de números... hasta que lo intentaron con nuestro querido p.
La cuestión es: partiendo de un segmento de longitud 1, ¿podemos construir con regla y compás un segmento que tenga longitud p?
En realidad este problema se puede plantear de otra manera más glamurosa que es la que le da nombre: dado un círculo de radio 1, ¿podemos construir con regla y compás un cuadrado que tenga su misma área?
 |
| ¿Podemos conseguir la cuadratura del círculo? |
En 1882, más de 2000 años después de que hubiera sido planteado, tras haber resistido a los mejores matemáticos del mundo durante dos milenios, el problema fue derrotado: Carl Louis Ferdinand von Lindemann (Lindemann para los amigos) se ganó la inmortalidad demostrando que NO, que LA CUADRATURA DEL CÍRCULO ES IMPOSIBLE (y por eso, igual ya lo habéis oído alguna vez, es por lo que se emplea el dicho, "eso es la cuadratura del círculo", para referirse a algo que es imposible de hacer).
Por cierto, id sacando los pañuelos de papel, porque no me cabe ninguna duda de que con lo que ahora mismo os voy a decir vuestros ojos se van a inundar de lágrimas de emoción sincera: ¿sabéis cómo consiguió resolver Lindemann el problema de la cuadratura del círculo? Con ecuaciones. Y ahora viene lo mejor, ¿sabéis qué tipo de ecuaciones? ¡Ecuaciones con polinomios!
Y cuando se os pase la emoción, Nuria, Paula, Fernando, Miguel, Álex y Adrián, aquí va el último reto (mandadme una imagen por Instagram o enseñádmelo en clase):
Reto IV de p. Construye con regla y compás:
- Un segmento de longitud raíz de 5.
- Un segmento de longitud raíz de 3.
El plazo termina el próximo jueves de 4 de abril.
Para poneros los dientes largos
y, por si tenéis curiosidad, aquí os enlazo una entrada del blog Gaussianos que recopila información sobre las construcciones con regla y compás:
martes, 26 de marzo de 2019
1º de ESO: "el colchón"
Espero que os hayáis fabricado un colchón mullidito para el próximo examen, pero lo más importante es detectar en qué os habéis equivocado y mejorar.
2º de ESO: examen de funciones
Os cuelgo los exámenes:
Quiero que cada uno hagáis el examen del otro grupo y me lo entreguéis en clase: los recogeré el viernes.
| Examen de 2º B | Solución |
|---|---|
| Examen de 2º C | Solución |
Quiero que cada uno hagáis el examen del otro grupo y me lo entreguéis en clase: los recogeré el viernes.
viernes, 22 de marzo de 2019
Pi (Tercera parte)
Recordad de la anterior entrada del reto:
Vemos que hay una gran diferencia entre las dos sumas. Cierto que las dos se van acercando más al valor de p cuantos más números sumamos, pero parece claro que una es mucho más rápida que la otra. Por ejemplo, al sumar 30000 números con la suma de Leibniz sabemos que p está entre 3'14156 y 3'14163, es decir, tenemos sólo 3 cifras exactas de p; con la de Nilakantha llegamos hasta 3’141592653589, 12 cifras exactas de p.
Y ahí precisamente están las dos claves que marcaron (y siguen marcando) la carrera por conseguir cifras decimales de p:
1) Hay que utilizar sumas que se acerquen lo más rápido posible al verdadero valor de p. En la actualidad se emplea una en la que cada vez que sumamos un número conseguimos 14 decimales exactos de p. Aquí nos lo cuentan:
2) Mi ordenador habrá tardado una fracción de segundo en hacer las cuentas. Para intentar batir el record de cifras de p se utilizan potentes ordenadores.
Vamos a ver algunos momentos importantes en la "Carrera de p":
- La mente más brillante en la historia de la Humanidad, Isaac Newton, dijo: "La naturaleza se reduce a un número: p. Quien descubra el misterio de p comprenderá el pensamiento de Dios", y tal vez por eso pasó unas cuantas tardes haciendo cuentas y calculó 15 decimales exactos... para lamentarse a continuación por haber perdido el tiempo haciendo cuentecitas inútiles.
- El aficionado a las matemáticas William Shanks dedicó casi 20 años de su vida a hacer cuentas para calcular 707 cifras decimales exactas de p... o eso creía: 70 años después, en 1944, usando una calculadora mecánica, se comprobó que "sólo" eran correctas hasta la 527.
- Una figura especial en el cálculo de las cifras de p es el portento indio Srinivasa Ramanujan, que encontró sumas de números que se acercaban muy rápido al valor de p (el algoritmo de Chudnovsky se basa en un descubrimiento suyo). Os dejo una de sus genialidades (a ver si sois capaces de hacer bien la cuenta -con calculadora, claro-):
- Con la llegada de los ordenadores la carrera quedó en manos de los informáticos. Precisamente la semana pasada se batió el récord llegando a más de 31 billones de cifras. Para ello la informática japonesa Emma Haruka Iwao ejecutó el programa y-cruncher en 25 ordenadores durante 121 días. Escritas seguidas en el tamaño que estáis leyendo darían más de 150 vueltas a la Tierra.
Dos cositas para terminar:
- Sí, es una gran pérdida de tiempo y de electricidad tener 25 potentes máquinas dedicadas 121 días a hacer algo que no sirve para nada. Afortunadamente los ordenadores se emplean casi siempre para cosas mucho más importantes. Os enlazo un vídeo muy interesante:
- p también inspira a los "poetas":
¿Feo? Bueno, eso es porque la gracia está en que al contar las letras de cada palabra obtenemos las 20 primeras cifras decimales de p.
 |
| Suma de Leibniz |
 |
| Suma de Nilakantha |
En la siguiente tabla podéis ver cómo van evolucionando las sumas anteriores según vamos añadiendo más números (en amarillo las cinco que os mandé como reto). Yo (mi ordenador más bien) he seguido sumando hasta los 30000 números. Por cierto, la segunda se llama suma de Nilakantha).
El valor real es p = 3’1415926535897932384...
Vemos que hay una gran diferencia entre las dos sumas. Cierto que las dos se van acercando más al valor de p cuantos más números sumamos, pero parece claro que una es mucho más rápida que la otra. Por ejemplo, al sumar 30000 números con la suma de Leibniz sabemos que p está entre 3'14156 y 3'14163, es decir, tenemos sólo 3 cifras exactas de p; con la de Nilakantha llegamos hasta 3’141592653589, 12 cifras exactas de p.
Y ahí precisamente están las dos claves que marcaron (y siguen marcando) la carrera por conseguir cifras decimales de p:
1) Hay que utilizar sumas que se acerquen lo más rápido posible al verdadero valor de p. En la actualidad se emplea una en la que cada vez que sumamos un número conseguimos 14 decimales exactos de p. Aquí nos lo cuentan:
2) Mi ordenador habrá tardado una fracción de segundo en hacer las cuentas. Para intentar batir el record de cifras de p se utilizan potentes ordenadores.
Vamos a ver algunos momentos importantes en la "Carrera de p":
- La mente más brillante en la historia de la Humanidad, Isaac Newton, dijo: "La naturaleza se reduce a un número: p. Quien descubra el misterio de p comprenderá el pensamiento de Dios", y tal vez por eso pasó unas cuantas tardes haciendo cuentas y calculó 15 decimales exactos... para lamentarse a continuación por haber perdido el tiempo haciendo cuentecitas inútiles.
- El aficionado a las matemáticas William Shanks dedicó casi 20 años de su vida a hacer cuentas para calcular 707 cifras decimales exactas de p... o eso creía: 70 años después, en 1944, usando una calculadora mecánica, se comprobó que "sólo" eran correctas hasta la 527.
- Una figura especial en el cálculo de las cifras de p es el portento indio Srinivasa Ramanujan, que encontró sumas de números que se acercaban muy rápido al valor de p (el algoritmo de Chudnovsky se basa en un descubrimiento suyo). Os dejo una de sus genialidades (a ver si sois capaces de hacer bien la cuenta -con calculadora, claro-):
Dos cositas para terminar:
- Sí, es una gran pérdida de tiempo y de electricidad tener 25 potentes máquinas dedicadas 121 días a hacer algo que no sirve para nada. Afortunadamente los ordenadores se emplean casi siempre para cosas mucho más importantes. Os enlazo un vídeo muy interesante:
- p también inspira a los "poetas":
Soy y seré a todos definible
mi nombre tengo que daros
cociente diametral siempre inmedible
soy de los redondos aros.
¿Feo? Bueno, eso es porque la gracia está en que al contar las letras de cada palabra obtenemos las 20 primeras cifras decimales de p.
Reto III de p: Tenéis que escribir algo con sentido de entre 20 y 30 palabras (a ver si os sale poético, sabio y/o gracioso). El plazo termina el próximo jueves 4 de marzo.
Aunque son de mi época supongo que los conocéis:
Por si os sirve de ayuda aquí os enlazo:
¡Superad esto!
Uffffff, yo lo odiaba, ¡qué aburrido era! (Pero acabo de ver este vídeo y me he desternillado de risa de lo malo que es):
jueves, 21 de marzo de 2019
1º de ESO: preparando el "colchón"
Va:
- el próximo martes haremos un control de operaciones clavado a los dos del año pasado:
- también os enlazo las soluciones de la hoja de operaciones que os repartí en clase:
- el próximo martes haremos un control de operaciones clavado a los dos del año pasado:
| Control 1 | Solución |
|---|---|
| Control 2 | Solución |
- también os enlazo las soluciones de la hoja de operaciones que os repartí en clase:
- y aquí os dejo las soluciones de la Autoevaluación que hoy hemos estado haciendo en clase. Corregidla (a lo bruto, a bien o mal) y fijaos atentamente en cuáles han sido los errores que habéis cometido.
¡¡DADLE FUERTE!!
(P.D.) Queridos míos del B, en el fondo (aunque sea muy, muy, muy, muy... allá a lo lejos en el fondo), ¿os gusta cuando me toca ir en las guardias, no? Esas caras de fastidio y resignación, esos suspiros lastimeros, ese decirle a Siridia, "por favor, que no venga David", ¿todo eso es broma, verdad?
viernes, 15 de marzo de 2019
1º de BHCS: apuntes de variables bidimensionales
Aquí os dejo las dispositivas de clase y la Hoja de cálculo:
y aquí un ejemplo de examen:
jueves, 14 de marzo de 2019
¡Feliz Día de Pi!
Sigue el reto:
- Tenéis hasta esta noche para completar la primera prueba. A ver si os animáis alguno a pelearle la camiseta a Álex (que está lanzado y ya ha hecho las tres primeras pruebas).
- Aquí os enlazo las dos siguientes. Tenéis de tiempo para responder hasta el próximo jueves 21 de marzo (¡ya llega la primavera!) a las 23:59.
EXTRA: en la segunda prueba se pide que aproximéis Pi calculando el área de dos cuadrados. Os animo a que lo intentéis también con dos hexágonos. Os doy una pista con la siguiente imagen:
- Tenéis hasta esta noche para completar la primera prueba. A ver si os animáis alguno a pelearle la camiseta a Álex (que está lanzado y ya ha hecho las tres primeras pruebas).
- Aquí os enlazo las dos siguientes. Tenéis de tiempo para responder hasta el próximo jueves 21 de marzo (¡ya llega la primavera!) a las 23:59.
EXTRA: en la segunda prueba se pide que aproximéis Pi calculando el área de dos cuadrados. Os animo a que lo intentéis también con dos hexágonos. Os doy una pista con la siguiente imagen:
miércoles, 13 de marzo de 2019
1º de BHCS: material de regresión lineal
Aquí os dejo:
Si tenéis algún problema con la Hoja de cálculo me lo decís y os la cuelgo en OpenOffice.
domingo, 10 de marzo de 2019
Día de Pi: concurso de la camiseta
 |
| 3-14 (mes-día) es 14 de marzo para los yanquis |
¿Cómo lo vamos a celebrar en vuestro blog favorito? Con un concurso cuyo premio será una magnífica camiseta.
 |
| El ganador elegirá color, diseño, etc. |
¿Qué hay que hacer? Leerse este previo:
y responder en los comentarios de la entrada al reto que se plantea antes de este próximo jueves 14 de marzo a las 23:59.
Después vendrán cuatro retos más, uno a la semana. Los que los respondáis todos correctamente, participaréis en el sorteo de una camiseta de Pi.
(P.D.) A veces me preguntáis que para qué sirve estudiar matemáticas. Por ejemplo, para que no os pasen cosas como a las del vídeo:
lunes, 4 de marzo de 2019
1º de BHCS: examen global de la 2ª evaluación
Dadle un repaso cuanto antes para que mejoréis el nivel: tanto los que tengáis que hacer la recuperación como los que hayáis aprobado (sobre todo si la cosa ha ido muy justa). En 2º esto aparece de nuevo con una vuelta más de tuerca.
Suscribirse a:
Comentarios
(
Atom
)