¡Feliz verano!

Nos vemos en septiembre

Poyekhali!

Apollo 11

Neil Armstrong, el primer hombre en pisar la Luna (¡me encanta esta foto!)

Neil Armstrong – Apollo 11 (julio de 1969).
Edwin “Buzz” Aldrin – Apollo 11 (julio de 1969).
Charles Conrad – Apollo 12 (noviembre de 1969).
Alan L. Bean – Apollo 12 (noviembre de 1969)
Alan Shepard – Apollo 14 (febrero de 1971).
Edgar Mitchell – Apollo 14 (febrero de 1971).
David Scott – Apollo 15 (julio de 1971).
James B. Irwin – Apollo 15 (julio de 1971).
John Young – Apollo 16 (abril de 1972).
Charles Duke – Apollo 16 (abril de 1972).
Harrison Schmitt – Apollo 17 (diciembre de 1972).
Eugen Cernan – Apollo 17 (diciembre de 1972).

Dentro de poco más de un mes se cumplirá el 50 aniversario de uno de los momentos cumbre de la Historia, la llegada del hombre a la Luna. Gracias a que fui sietemesino (por favor, no digáis, ¡y fíjate lo grande que eres ahora!, que he oído esa frase un millón de veces), por veintipocos días puedo decir que ha habido seres humanos ahí arriba estando yo vivo (y os contaré que la cosa estuvo muy chunga para mí por aquel entonces: qué cerca "estuvisteis" de libraros de mí, ¡y vosotros sin saberlo!).

Para un niño (el que fui y la parte cada vez más pequeña que me va quedando) entusiasmado con los viajes espaciales, estos 50 años han sido una agonía. Cuántas noches mirando al cielo fantaseando con que algún día iría ahí. Cuántas revistas leídas compulsivamente una y otra vez (¡si ya me las sabía de memoria!) con planes americanos y soviéticos para ir a Marte. Qué pequeñas satisfacciones los éxitos de algunas sondas. Desde hace unos años me lamo las heridas enganchado a este blog:

Eureka

Estos últimos días os he puesto en clase el vídeo de la pluma y el martillo y me he sentido fatal. No recuerdo esa sensación otros años y el caso es que la cosa fue igual: ¡la inmensa mayoría tenéis el mismo entusiasmo espacial que mis gatos!

Cuando la Unión Soviética lanzó en 1957 el primer satélite artificial, en todo el mundo se produjo una explosión de entusiasmo por la ciencia y gracias a ello muchos niños y jóvenes se hicieron matemáticos, físicos, ingenieros... De hecho en Estados Unidos este fenómeno se conoce como efecto Sputnik -el nombre del satélite-.

A la espera de que la próxima década se confirmen algunas intenciones de vuelta a la Luna (que necesitarán acciones decididas -y mucho dinero- o se quedarán en eso), que despierten e incentiven vuestro entusiasmo científico, dejadme intentarlo proponiéndoos un reto facilito.

Primera foto de la Tierra y la Luna flotando en el espacio. Sonda Voyager 1.

Reto de la Luna: ¿cuántas veces tenemos que doblar un folio de grosor 0'1 milímetro para "llegar" de la Tierra a la Luna?

Entre los que contestéis correctamente (aquí en los comentarios del blog) sortearé 3 entradas de cine para ver:

que se estrena, cómo no, el próximo 16 de julio.

Exámenes del curso 2018/2019

1º de ESO

Números naturales	Solución
Potencias y raíces	Solución
Divisibilidad_1B	Solución
Divisibilidad_1C	Solución
Global 1ª EV_1B	Solución
Global 1ª EV_1C	Solución
Operaciones con decimales	Solución
Problemas	Solución
Operaciones con fracciones	Solución
Fracciones	Solución
Proporcionalidad y porcentajes_1B	Solución
Proporcionalidad y porcentajes_1C	Solución
Global 2ª EV_1B	Solución
Global 2ª EV_1C	Solución
Operaciones algebraicas	Solución
Álgebra	Solución
Geometría	Solución
Global 3ª EV	Solución

2º de ESO

Números naturales y enteros_2B	Solución
Números naturales y enteros_2C	Solución
Números reales	Solución
Fracciones, proporcionalidad, incrementos	Solución
Global 1ª EV	Solución
Operaciones algebraicas	Solución
Ecuaciones	Solución
Sistemas de ecuaciones	Solución
Global 2ª EV_2B	Solución
Global 2ª EV_2C	Solución
Funciones_2B	Solución
Funciones_2C	Solución
Pitágoras y semejanza_2B	Solución
Pitágoras y semejanza_2C	Solución
Áreas y volúmenes	Solución
Global 3ª EV	Solución

2º de ESO: examen global de la 3ª evaluación

Mañana vemos cómo ha salido.

Examen

Solución

1º de ESO: examen global de la 3ª evaluación

Mañana vemos cómo ha salido y hablamos de lo que nos queda (porque espero que lo tengáis claro: ¡esto no se ha acabado!).

Examen

Solución

1º de BHCS: examen global de la 3ª evaluación

Aquí lo tenéis.

Examen

2º de ESO: control de áreas y volúmenes

Aquí lo tenéis.

Examen

Solución

2º de ESO: apuntes de Estadística y Probabilidad

Os dejo los apuntes de clase y la solución al ejercicio propuesto:

Apuntes de Estadística

Solución al ejercicio propuesto

Apuntes de Probabilidad

1º de ESO: apuntes de Estadística y Probabilidad

¡Esto se está acabando!

Apuntes

Solución al ejercicio

Concurso de acertijos matemáticos

Para celebrar que el 12 de mayo es el Día Escolar de las Matemáticas dos alumnos de la UR han convocado un Concurso de Acertijos Matemáticos:

Enlace a la convocatoria

Resumiendo, tenéis que:

- resolver estos seis acertijos:

Enlace a los acertijos

- y enviar las soluciones (de los que consigáis hacer) antes del domingo 26 de mayo de 2019 a las 14:00 horas a la dirección:

concurso.acertijos.matematicos@gmail.com

indicando:

Asunto del correo: Concurso de acertijos matemáticos.
Nombre, apellidos y nº de DNI.
Documento legible en el que se encuentren las soluciones detalladas de los acertijos.

El ganador se llevará 50 euros en metálico.

¡¡ANIMAOS!!

1º de BHCS: examen de probabilidad y v.a. discretas

Hacedlo en casa y el lunes resolvemos las dudas que puedan quedar:

Examen

1º de BHCS: variables aleatorias

Os cuelgo las diapositivas que hemos utilizado en clase:

Variables discretas: Binomial

Variables continuas: Normal

y las:

Tablas de probabilidad

El Olimpo de los números

Lo primero es lo primero:

¡Bien hecho Adrián!

Desde un punto de vista matemático, ¿cuáles son los números más importantes, los dioses del Olimpo? Aquí tenéis juntos a "los cinco magníficos" en la famosa identidad de Euler:

¡Preciosa para un tatuaje!

Adoremos a las divinidades:

0 El cero es el elemento neutro de la suma, es decir, si a cualquier número le sumo un 0, el número no cambia. Por ejemplo: 13 = 13 + 0.

1 El uno es el elemento neutro de la multiplicación, es decir, si un número lo multiplico por 1, el número no cambia. Por ejemplo: 13 = 13 x 1.

p De éste ya hemos hablado bastante, ¿verdad? Os recuerdo la idea original:

Si tenemos una circunferencia (pensemos que es una rueda) de 1 metro de diámetro y la hacemos rodar una vuelta entera, recorremos una distancia de p metros, es decir, 3'14159... metros, 3 veces y un poco el diámetro de la circunferencia.

Hasta aparece en la Biblia:

Diámetro = 10; Longitud = 30 (y pico)

e Coged una calculadora e id haciendo estas cuentas:

Si "no paráis nunca" llegaréis al valor exacto de:

e = 2,718281828459045235360287...

Estas cuentecillas aparecieron por primera vez en un problema de economía en el siglo XVII y desde entonces en muchos otros sitios. No sé si vais a pillar la idea pero Eduardo siempre cuenta las cosas con gracia:

i Ya os hablé de él (Los números imaginarios). Aquí os lo explica mejor nuestro divulgador favorito:

1º de ESO: examen de geometría

Como siempre os digo, no hay mejor momento para aprender, para mejorar, para resolver las dudas que todavía os queden, que justo ahora. Haced el examen y consultad después la solución.

Examen

Solución

Pasadlo bien esta Semana Santa, descansad... pero no os olvidéis de mí, que os espero a la vuelta para presentaros a vuestras futuras amigas las funciones. ¿Que qué son las funciones?

¡Esto es una función!

2º de ESO: examen de Pitágoras y semejanza

Os cuelgo los exámenes:

Examen de 2º B	Solución
Examen de 2º C	Solución

Quiero que estas vacaciones hagáis en casa los dos. Los recogeré justo a la vuelta.

¡FELIZ SEMANA SANTA!

No me vengáis con cuentos ni canciones

Ni os molesteis en intentarlo:

porque sólo tengo una cosa que deciros:

1º de ESO: preparando el examen de geometría

Os cuelgo los exámenes de geometría de los dos cursos anteriores (y también los correspondientes exámenes globales de la 3ª evaluación, que contienen más preguntas de este tema). Supongo que el que os pondré el próximo miércoles tendrá un formato parecido.

Examen de geometría 16/17	Solución
Examen de geometría 17/18	Solución
Examen Global 3ª EV 16/17	Solución
Examen Global 3ª EV 17/18	Solución

Como os digo siempre, primero machacad lo básico: ángulos, Pitágoras, figuras elementales (trapecios, rombos, pentágonos, hexágonos...) y luego ya, cuando eso lo tengáis totalmente controlado, os metéis con las figuras más complejas.

1º de ESO: figuras geométricas

Aquí os cuelgo unas diapositivas para que les peguéis un vistazo. Algunas de estas cosas las habéis dado en Plástica. Sólo me interesa que os suenen. Lo que vayamos a utilizar os lo recalcaré en clase:

Figuras geométricas

Os cuelgo también la solución del controlillo de ángulos:

Solución

1º de ESO: solución al "controlillo casero" de ángulos y Pitágoras

El lunes me decís cómo os ha salido y resolvemos las dudas (sí, ya lo sé, el martes los del C) .

Solución

Por cierto, que no se os olvide practicar las cuentecitas con ángulos que el martes tenemos otro "controlillo", y cuando pregunte "¿éxitos", ¡os quiero a todos manos arriba!

************

En mates, de chaval en el colegio, odiaba tener que memorizar cosas (y eso que tenía bastante buena memoria). Con esto de los ángulos hay muchos nombres. No me los aprendí entonces, y cada año que lo explico tengo que mirarlos porque mi cerebro se niega a almacenar este tipo de información.

Los pongo aquí para tenerlos a tiro cuando alguien, vosotros o yo, necesite recordarlos:

Ángulos según tamaño

Parejas: según su suma (suplementarios y complementarios) y opuestos por el vértice

Ángulos alternos: internos y externos

Mapamundi

Si nos piden que pensemos en un mapa de nuestro planeta, a la mayoría nos viene algo así a la cabeza:

Mapamundi de Mercator

Y si a la vista del mismo nos preguntaran, por ejemplo, ¿qué es más grande, Groenlandia o África?, tendríamos que pensarnos la respuesta... aunque en realidad no hay mucho que pensar:

- Superficie de Groenlandia = 2'2 millones de km.

- Superficie de África = 30'4 millones de km.

Sí, África es unas 14 veces mayor que Groenlandia. ¡¿Qué está pasando aquí?!

Naturalmente todo tiene una explicación (¡matemática!) y es la siguiente:

No es posible representar, de forma semejante, la superficie de una esfera (y la Tierra lo es) en un plano. Es decir, podemos hacer "una especie de boceto", pero siempre habrá alguna distorsión.

El mapamundi más habitual (el de arriba) se basa en la proyección cartográfica de Mercator, que tiene la pega de que aumenta el tamaño de las regiones más cercanas a los polos.

Hay muchas otras opciones aunque todas tienen sus pegas. Por ejemplo, los dos siguientes respetan mejor los tamaños de las regiones terrestres (¿cómo veis ahora lo de África y Groenlandia?), pero el primero es un lío para las distancias por mar y en el segundo es muy difícil orientarse:

Os enlazo dos artículos sobre este tema y otras curiosidades:

Todos los mapas que conoces están mal

El mapa que mejor respeta las proporciones también está mal

¡Gracias!

¿Cómo voy a hacer un sorteo? Para un profesor lo más bonito que existe es el interés y el esfuerzo de sus alumnos. Si además ha habido reencuentros que han significado un emocionante homenaje a los "viejos" y buenos tiempos, sólo os puedo decir:

¡ELEGID LA QUE MÁS OS GUSTE!

¡Que aparezca Pi, claro! Me decís todas las características, yo la pido, y os la entrego. Enlazo un par de posibilidades, pero podéis buscar por vuestra cuenta (¡por favor, escoged la que más os guste, que ese sea el único criterio! ¡NO miréis el precio!).

La Tostadora

Amazon

Me decís en persona, Instagram o mensaje en esta entrada.

De corazón:

¡GRACIAS!

1º de BHCS: examen de estadística bidimensional

Aquí os lo dejo:

Examen

Intentad hacerlo en casa y el viernes resolvemos las dudas que sigan quedando.

1º de ESO: examen de álgebra

Aquí lo tenéis. Seguid dándole a esto porque en el examen global aparecerán polinomios, ecuaciones y problemas... y en 2º de ESO hay una evaluación entera dedicada al álgebra, así que tenéis que coger el máximo nivel posible.

Examen

 

Solución

Construyendo mi ataud

 Corpus hypercubus, de Salvador Dalí

Mido 1'94 y, cuando muera (¡lo que tengo que hacer para captar vuestra atención!), me gustaría que mi ataúd tuviese forma hipercúbica de 1 centímetro de arista. ¿En qué dimensión empieza a ser eso posible?

Primero vamos a responder a tres preguntas (los de 2º ya las sabéis; los de 1º las entenderéis dentro de poco, cuando veamos el Teorema de Pitágoras):


1) ¿Cuánto mide el segmento más largo que puedo pintar encima de un segmento de 1 centímetro?

La respuesta es fácil, como mucho, encima de ése, podré pintar otro segmento que mida 1 centímetro.

2) ¿Cuánto mide el segmento más largo que puedo pintar en un papelito cuadrado de 1 centímetro de lado?

Claramente el segmento más largo que podemos pintar es la diagonal del cuadrado. Llamamos a Pitágoras:

Es decir, como mucho podemos pintar un segmento de longitud raíz de 2 = 1'4142... centímetros.


3) ¿Cuánto mide la varilla más larga que puedo meter dentro de un cubo de 1 centímetro de arista?

Es muy parecido al caso anterior: lo más largo de un cubo es su diagonal, y podemos calcular su longitud aplicando Pitágoras (notad que las diagonales de las caras, que son cuadrados, miden raíz de 2):

Es decir, la varilla más larga que cabe mide raíz de 3 = 1'732...


Conclusiones:

- en un segmento de 1 cm (dejadme rebautizarlo: "hipercubo de dimensión 1" con "arista" 1 cm), lo más grande que "cabe dentro" puede medir 1 cm,

- en un cuadrado de 1 cm de lado ("hipercubo de dimensión 2" con "arista" 1 cm), lo más grande que "cabe dentro" (en la diagonal) puede medir raíz de 2 = 1'4142... cm,

- en un cubo de 1 cm de arista ("hipercubo de dimensión 3" con arista 1 cm), lo más grande que "cabe dentro" (en la diagonal) puede medir raíz de 3 = 1'732... cm.

Efectivamente, esto sigue, y aunque hacer dibujos es (casi) imposible, las cuentas salen igual de fáciles y queda claro que las diagonales van siendo cada vez más y más largas:

- en un hipercubo de dimensión 4 con arista 1 cm, lo más grande que "cabe dentro" (en la diagonal) puede medir raíz de 4 = 2 cm,

- en un hipercubo de dimensión 5 con arista 1 cm, lo más grande que "cabe dentro" (en la diagonal) puede medir raíz de 5 = 2'236... cm,

- en general, en un hipercubo de dimensión n con arista 1 cm, lo más grande que "cabe dentro" (en la diagonal) puede medir raíz de n cm.

Responded ahora: ¿de qué dimensión tenéis que construir un "hiperataúd" de 1 cm de arista para que quepa un profesor de matemáticas de 194 cm?


Nota final: he dicho antes que los dibujos son casi imposibles. De igual manera que en las fotos o en los cuadros representamos en 2 dimensiones (utilizando la perspectiva) la realidad de 3 dimensiones (fijaos también en cómo dibujamos un cubo), en 3 dimensiones pueden hacerse representaciones del hipercubo de 4 dimensiones. Son ejemplos el cuadro de Dalí del principio o algunos monumentos (haced clic en las imágenes para saber algo más de ellos):

Monumento de la Constitución, en Madrid

Arco de la Defensa, en París

"Dibujo" de un hipercubo 4D

Booktubers

Pi (final): la cuadratura del círculo

Los matemáticos de la antigua Grecia se inventaron el “juego de la regla y el compás” en el que, siguiendo unas determinadas normas, había que construir figuras geométricas, dividir segmentos o ángulos en varias partes iguales, etc, utilizando una regla y un compás. No vamos a entrar en detalles pero una de las normas es que la regla no tiene marcas, no sirve para medir, sólo se puede utilizar para pintar segmentos o rectas uniendo dos puntos.

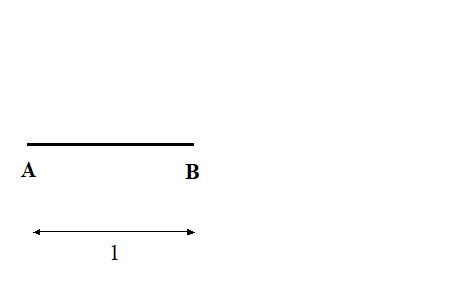
Una de las modalidades del “juego de la regla y el compás” era la de construir números. La idea es sencilla: partimos de un papel en el que tenemos dibujado un segmento de longitud 1 (da igual la unidad; por comodidad ponemos nombre a los extremos, A y B):

y, utilizando un compás y una regla (insisto, sin números, no podemos medir con ella), tenemos que intentar construir segmentos de la longitud que nos digan. Vamos a ver tres ejemplos:

1) Construir un segmento de longitud 2. El 2 sale muy fácil: prolongamos por la derecha el segmento original con la regla, pinchamos con el compás en el punto B, lo abrimos hasta el punto A y lo giramos y marcamos el punto C. Desde A hasta C el segmento resultante mide 2.

Siguiendo la misma idea sería inmediato construir segmentos de longitudes 3, 4, 5, 6...

2) Construir un segmento de longitud 0'5. ¡Seguro que lo habéis hecho alguna vez! Simplemente se trata de dibujar la mediatriz del segmento que nos dan:

3) Construir un segmento de longitud raíz de 2. Lo tenemos a tiro aprovechando los ejemplos anteriores:

y ya lo tenemos, si recordamos el Teorema de Pitágoras:

Volvamos al dibujo anterior:

¿Cuánto mide el segmento DC?

Los griegos jugaron bastante a este juego y lograron construir un montón de números... hasta que lo intentaron con nuestro querido p.

La cuestión es: partiendo de un segmento de longitud 1, ¿podemos construir con regla y compás un segmento que tenga longitud  p?

En realidad este problema se puede plantear de otra manera más glamurosa que es la que le da nombre: dado un círculo de radio 1, ¿podemos construir con regla y compás un cuadrado que tenga su misma área?

¿Podemos conseguir la cuadratura del círculo?

En 1882, más de 2000 años después de que hubiera sido planteado, tras haber resistido a los mejores matemáticos del mundo durante dos milenios, el problema fue derrotado: Carl Louis Ferdinand von Lindemann (Lindemann para los amigos) se ganó la inmortalidad demostrando que NO, que LA CUADRATURA DEL CÍRCULO ES IMPOSIBLE (y por eso, igual ya lo habéis oído alguna vez, es por lo que se emplea el dicho, "eso es la cuadratura del círculo", para referirse a algo que es imposible de hacer).

Por cierto, id sacando los pañuelos de papel, porque no me cabe ninguna duda de que con lo que ahora mismo os voy a decir vuestros ojos se van a inundar de lágrimas de emoción sincera: ¿sabéis cómo consiguió resolver Lindemann el problema de la cuadratura del círculo? Con ecuaciones. Y ahora viene lo mejor, ¿sabéis qué tipo de ecuaciones? ¡Ecuaciones con polinomios!

Y cuando se os pase la emoción, Nuria, Paula, Fernando, Miguel, Álex y Adrián, aquí va el último reto (mandadme una imagen por Instagram o enseñádmelo en clase):

Reto IV de p. Construye con regla y compás:

• Un segmento de longitud raíz de 5.
• Un segmento de longitud raíz de 3.

El plazo termina el próximo jueves de 4 de abril.

Para poneros los dientes largos

y, por si tenéis curiosidad, aquí os enlazo una entrada del blog Gaussianos que recopila información sobre las construcciones con regla y compás:

Construcciones con regla y compás

1º de ESO: "el colchón"

Espero que os hayáis fabricado un colchón mullidito para el próximo examen, pero lo más importante es detectar en qué os habéis equivocado y mejorar.

Control de operaciones algebraicas

Solución

2º de ESO: examen de funciones

Os cuelgo los exámenes:

Examen de 2º B	Solución
Examen de 2º C	Solución

Quiero que cada uno hagáis el examen del otro grupo y me lo entreguéis en clase: los recogeré el viernes.

Pi (Tercera parte)

Recordad de la anterior entrada del reto:

Suma de Leibniz

Suma de Nilakantha

En la siguiente tabla podéis ver cómo van evolucionando las sumas anteriores según vamos añadiendo más números (en amarillo las cinco que os mandé como reto). Yo (mi ordenador más bien) he seguido sumando hasta los 30000 números. Por cierto, la segunda se llama suma de Nilakantha).

 El valor real es p = 3’1415926535897932384...

Vemos que hay una gran diferencia entre las dos sumas. Cierto que las dos se van acercando más al valor de p cuantos más números sumamos, pero parece claro que una es mucho más rápida que la otra. Por ejemplo, al sumar 30000 números con la suma de Leibniz sabemos que p está entre 3'14156 y 3'14163, es decir, tenemos sólo 3 cifras exactas de p; con la de Nilakantha llegamos hasta 3’141592653589, 12 cifras exactas de p.

Y ahí precisamente están las dos claves que marcaron (y siguen marcando) la carrera por conseguir cifras decimales de p:

1) Hay que utilizar sumas que se acerquen lo más rápido posible al verdadero valor de  p. En la actualidad se emplea una en la que cada vez que sumamos un número conseguimos 14 decimales exactos de p. Aquí nos lo cuentan:

El algoritmo de Chudnovsky

2) Mi ordenador habrá tardado una fracción de segundo en hacer las cuentas. Para intentar batir el record de cifras de p se utilizan potentes ordenadores.

Vamos a ver algunos momentos importantes en la "Carrera de  p":

- La mente más brillante en la historia de la Humanidad, Isaac Newton, dijo: "La naturaleza se reduce a un número: p. Quien descubra el misterio de p comprenderá el pensamiento de Dios", y tal vez por eso pasó unas cuantas tardes haciendo cuentas y calculó 15 decimales exactos... para lamentarse a continuación por haber perdido el tiempo haciendo cuentecitas inútiles.

- El aficionado a las matemáticas William Shanks dedicó casi 20 años de su vida a hacer cuentas para calcular 707 cifras decimales exactas de p... o eso creía: 70 años después, en 1944, usando una calculadora mecánica, se comprobó que "sólo" eran correctas hasta la 527.

- Una figura especial en el cálculo de las cifras de p es el portento indio Srinivasa Ramanujan, que encontró sumas de números que se acercaban muy rápido  al valor de p (el algoritmo de Chudnovsky se basa en un descubrimiento suyo). Os dejo una de sus genialidades (a ver si sois capaces de hacer bien la cuenta -con calculadora, claro-):

- Con la llegada de los ordenadores la carrera quedó en manos de los informáticos. Precisamente la semana pasada se batió el récord llegando a más de 31 billones de cifras. Para ello la informática japonesa Emma Haruka Iwao ejecutó el programa y-cruncher en 25 ordenadores durante 121 días. Escritas seguidas en el tamaño que estáis leyendo darían más de 150 vueltas a la Tierra.

Enlace a la lista de récords de cifras de p

Dos cositas para terminar:

- Sí, es una gran pérdida de tiempo y de electricidad tener 25 potentes máquinas dedicadas 121 días a hacer algo que no sirve para nada. Afortunadamente los ordenadores se emplean casi siempre para cosas mucho más importantes. Os enlazo un vídeo muy interesante:

El superordenador Mare Nostrum

- p también inspira a los "poetas":

Soy y seré a todos definible

mi nombre tengo que daros

cociente diametral siempre inmedible

soy de los redondos aros.

¿Feo? Bueno, eso es porque la gracia está en que al contar las letras de cada palabra obtenemos las 20 primeras cifras decimales de p. 

Reto III de p: Tenéis que escribir algo con sentido de entre 20 y 30 palabras (a ver si os sale poético, sabio y/o gracioso). El plazo termina el próximo jueves 4 de marzo.

Aunque son de mi época supongo que los conocéis:

Por si os sirve de ayuda aquí os enlazo:

Personajes de Barrio Sésamo

¡Superad esto!

Uffffff, yo lo odiaba, ¡qué aburrido era! (Pero acabo de ver este vídeo y me he desternillado de risa de lo malo que es):

1º de ESO: preparando el "colchón"

Va:

- el próximo martes haremos un control de operaciones clavado a los dos del año pasado:

Control 1	Solución
Control 2	Solución

- también os enlazo las soluciones de la hoja de operaciones que os repartí en clase:

Solución de la hoja de operaciones

- y aquí os dejo las soluciones de la Autoevaluación que hoy hemos estado haciendo en clase. Corregidla (a lo bruto, a bien o mal) y fijaos atentamente en cuáles han sido los errores que habéis cometido.

Solución de la Autoevaluación

¡¡DADLE FUERTE!!

(P.D.) Queridos míos del B, en el fondo (aunque sea muy, muy, muy, muy... allá a lo lejos en el fondo), ¿os gusta cuando me toca ir en las guardias, no? Esas caras de fastidio y resignación, esos suspiros lastimeros, ese decirle a Siridia, "por favor, que no venga David", ¿todo eso es broma, verdad?

1º de BHCS: apuntes de variables bidimensionales

Aquí os dejo las dispositivas de clase y la Hoja de cálculo:

Variables discretas y continuas

Estudio de variables discretas

Hoja de cálculo para variables discretas

 

y aquí un ejemplo de examen:

 

Ejemplo de examen

¡Feliz Día de Pi!

Sigue el reto:

- Tenéis hasta esta noche para completar la primera prueba. A ver si os animáis alguno a pelearle la camiseta a Álex (que está lanzado y ya ha hecho las tres primeras pruebas).

Primera prueba de la camiseta

- Aquí os enlazo las dos siguientes. Tenéis de tiempo para responder hasta el próximo jueves 21 de marzo (¡ya llega la primavera!) a las 23:59.

Segunda prueba de la camiseta

Tercera prueba de la camiseta

EXTRA: en la segunda prueba se pide que aproximéis Pi calculando el área de dos cuadrados. Os animo a que lo intentéis también con dos hexágonos. Os doy una pista con la siguiente imagen:

1º de BHCS: material de regresión lineal

Aquí os dejo:

Diapositivas que hemos usado en clase

Hoja de cálculo para la regresión lineal (Excel)

Si tenéis algún problema con la Hoja de cálculo me lo decís y os la cuelgo en OpenOffice.

Día de Pi: concurso de la camiseta

3-14 (mes-día) es 14 de marzo para los yanquis

¿Cómo lo vamos a celebrar en vuestro blog favorito? Con un concurso cuyo premio será una magnífica camiseta.

El ganador elegirá color, diseño, etc.

¿Qué hay que hacer? Leerse este previo:

Suma de infinitos números

y responder en los comentarios de la entrada al reto que se plantea antes de este próximo jueves 14 de marzo a las 23:59.

Después vendrán cuatro retos más, uno a la semana. Los que los respondáis todos correctamente, participaréis en el sorteo de una camiseta de Pi.

(P.D.) A veces me preguntáis que para qué sirve estudiar matemáticas. Por ejemplo, para que no os pasen cosas como a las del vídeo:

1º de BHCS: examen global de la 2ª evaluación

Dadle un repaso cuanto antes para que mejoréis el nivel: tanto los que tengáis que hacer la recuperación como los que hayáis aprobado (sobre todo si la cosa ha ido muy justa). En 2º esto aparece de nuevo con una vuelta más de tuerca.

Examen

2º de ESO: examen global de la 2ª evaluación

Os digo lo mismo que a los de 1º: la semana que viene vemos cómo os han salido y hablamos del futuro. Descansad este puente... bueno, los del C sólo un poquito.

Examen de 2º B	Solución
Examen de 2º C	Solución

Os cuelgo también la:

Solución al ejercicio propuesto de Resolución gráfica de ecuaciones

que me interesa mucho para el próximo tema.

1º de ESO: examen global de la 2ª evaluación

Examen de 1º B	Solución
Examen de 1º C	Solución

Enhorabuena a todos por el esfuerzo. La semana que viene vemos cómo os han salido y hablamos del futuro. Descansad este puente que os lo habéis ganado.

Sobre todo porque a la vuelta...

¡La 2ª evaluación ha muerto!

¡Viva la 3ª evaluación!

Aquí os dejo las diapositivas que vamos a utilizar en clase:

Introducción al Álgebra

2º de ESO: examen de sistemas de ecuaciones

Aquí lo tenéis.

Examen

Solución

Y os dejo un extra en el que os cuento un par de cosas.

Just for fun

1º de ESO: control de proporcionalidad, porcentajes, incrementos y disminuciones

Aquí los tenéis. Sólo tengo una cosa que deciros: ¡la próxima semana es el global!

Control de 1º B	Solución
Control de 1º C	Solución

1º de ESO: preparando el control de proporcionalidad, porcentajes, incrementos y disminuciones

Quiero que:

• Tengáis claro que, especialmente en este caso, el objetivo del examen/control es el de trabajar y mejorar más allá de sacar un 0, un 1... o un 10.

• Le peguéis un vistazo al examen del curso pasado porque los que os voy a poner este año serán similares: Examen y Solución.

• Repaséis los ejercicios de la hoja de clase. Aquí os dejo las soluciones:

Soluciones a los ejercicios

• Consejos finales:

•  Concentraos en dominar perfectamente los ejercicios de proporcionalidad (ya sabéis que lo más importante es detectar si la relación es directa o inversa).

•  Repasad los distintos ejercicios de porcentajes y daos cuenta de que son exactamente los mismos que hicimos con fracciones (los de parte, total y porcentaje, el problema "de la suma" y el problema "del producto" -alias el "del resto"-). 

• Un pelín más complicados son los problemas de incrementos y disminuciones. Intentad pillar la idea de la "regla de tres" con la que se pueden resolver todas las variantes. Yo os recomendaría que os hicieseis una hoja resumen como esta: