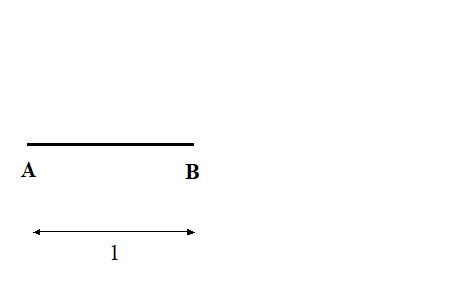
Una de las modalidades del “juego de la regla y el compás” era la de construir números. La idea es sencilla: partimos de un papel en el que tenemos dibujado un segmento de longitud 1 (da igual la unidad; por comodidad ponemos nombre a los extremos, A y B):
1) Construir un segmento de longitud 2. El 2 sale muy fácil: prolongamos por la derecha el segmento original con la regla, pinchamos con el compás en el punto B, lo abrimos hasta el punto A y lo giramos y marcamos el punto C. Desde A hasta C el segmento resultante mide 2.
 |
| Siguiendo la misma idea sería inmediato construir segmentos de longitudes 3, 4, 5, 6... |
2) Construir un segmento de longitud 0'5. ¡Seguro que lo habéis hecho alguna vez! Simplemente se trata de dibujar la mediatriz del segmento que nos dan:
3) Construir un segmento de longitud raíz de 2. Lo tenemos a tiro aprovechando los ejemplos anteriores:
y ya lo tenemos, si recordamos el Teorema de Pitágoras:
Volvamos al dibujo anterior:
Los griegos jugaron bastante a este juego y lograron construir un montón de números... hasta que lo intentaron con nuestro querido p.
La cuestión es: partiendo de un segmento de longitud 1, ¿podemos construir con regla y compás un segmento que tenga longitud p?
En realidad este problema se puede plantear de otra manera más glamurosa que es la que le da nombre: dado un círculo de radio 1, ¿podemos construir con regla y compás un cuadrado que tenga su misma área?
En 1882, más de 2000 años después de que hubiera sido planteado, tras haber resistido a los mejores matemáticos del mundo durante dos milenios, el problema fue derrotado: Carl Louis Ferdinand von Lindemann (Lindemann para los amigos) se ganó la inmortalidad demostrando que NO, que LA CUADRATURA DEL CÍRCULO ES IMPOSIBLE (y por eso, igual ya lo habéis oído alguna vez, es por lo que se emplea el dicho, "eso es la cuadratura del círculo", para referirse a algo que es imposible de hacer).
Por cierto, id sacando los pañuelos de papel, porque no me cabe ninguna duda de que con lo que ahora mismo os voy a decir vuestros ojos se van a inundar de lágrimas de emoción sincera: ¿sabéis cómo consiguió resolver Lindemann el problema de la cuadratura del círculo? Con ecuaciones. Y ahora viene lo mejor, ¿sabéis qué tipo de ecuaciones? ¡Ecuaciones con polinomios!
Y cuando se os pase la emoción, Nuria, Paula, Fernando, Miguel, Álex y Adrián, aquí va el último reto (mandadme una imagen por Instagram o enseñádmelo en clase):
Reto IV de p. Construye con regla y compás:
y ya lo tenemos, si recordamos el Teorema de Pitágoras:
Volvamos al dibujo anterior:
 |
| ¿Cuánto mide el segmento DC? |
Los griegos jugaron bastante a este juego y lograron construir un montón de números... hasta que lo intentaron con nuestro querido p.
La cuestión es: partiendo de un segmento de longitud 1, ¿podemos construir con regla y compás un segmento que tenga longitud p?
En realidad este problema se puede plantear de otra manera más glamurosa que es la que le da nombre: dado un círculo de radio 1, ¿podemos construir con regla y compás un cuadrado que tenga su misma área?
 |
| ¿Podemos conseguir la cuadratura del círculo? |
En 1882, más de 2000 años después de que hubiera sido planteado, tras haber resistido a los mejores matemáticos del mundo durante dos milenios, el problema fue derrotado: Carl Louis Ferdinand von Lindemann (Lindemann para los amigos) se ganó la inmortalidad demostrando que NO, que LA CUADRATURA DEL CÍRCULO ES IMPOSIBLE (y por eso, igual ya lo habéis oído alguna vez, es por lo que se emplea el dicho, "eso es la cuadratura del círculo", para referirse a algo que es imposible de hacer).
Por cierto, id sacando los pañuelos de papel, porque no me cabe ninguna duda de que con lo que ahora mismo os voy a decir vuestros ojos se van a inundar de lágrimas de emoción sincera: ¿sabéis cómo consiguió resolver Lindemann el problema de la cuadratura del círculo? Con ecuaciones. Y ahora viene lo mejor, ¿sabéis qué tipo de ecuaciones? ¡Ecuaciones con polinomios!
Y cuando se os pase la emoción, Nuria, Paula, Fernando, Miguel, Álex y Adrián, aquí va el último reto (mandadme una imagen por Instagram o enseñádmelo en clase):
Reto IV de p. Construye con regla y compás:
- Un segmento de longitud raíz de 5.
- Un segmento de longitud raíz de 3.
El plazo termina el próximo jueves de 4 de abril.
Para poneros los dientes largos
y, por si tenéis curiosidad, aquí os enlazo una entrada del blog Gaussianos que recopila información sobre las construcciones con regla y compás:




No hay comentarios :
Publicar un comentario